▶정규화 정의
이상현상이 발생하는 테이블을 수정하여 정상으로 만드는 과정
-이상현상: 테이블에 투플을 삽입할 때 부득이하게 NULL 값이 입력되거나(삽입이상), 삭제 시 연쇄삭제 현상이 발생하거나(삭제이상), 수정 시 데이터의 일관성이 훼손되는 현상(수정이상)
▶함수 종속성
| 학생번호 | 학생이름 | 주소 | 학과 | 학과사무실 | 강좌이름 | 강의실 | 성적 |
| 501 | 박지성 | 영국 맨체스타 | 컴퓨터과 | 공학관101 | 데이터베이스 | 공학관110 | 3.5 |
| 401 | 김연아 | 대한민국 서울 | 체육학과 | 체육관101 | 데이터베이스 | 공학관110 | 4.0 |
| 402 | 장미란 | 대한민국 경기도 | 체육학과 | 체육관101 | 스포츠경영 | 체육관103 | 3.5 |
| 502 | 추신수 | 미국 클리블랜드 | 컴퓨터과 | 공학관101 | 자료구조 | 공학관111 | 4.0 |
| 501 | 박지성 | 영국 맨체스타 | 컴퓨터과 | 공학관101 | 자료구조 | 공학관 111 | 3.5 |
<학생수강성적 릴레이션>
위의 릴레리션(테이블)의 각 속성 사이에는 의존성이 존재한다. 예를 들어 강좌이름이 '데이터 베이스'인 경우 강의실은 '공학과 110'호 한 곳 뿐이다.
반면 학생이름이 '박지성'인 경우 강좌이름은 '데이터베이스'도 있고 '자료구조'도 있다. 강의실은 강좌이름만 알면 바로 알 수 있지만 강좌이름은 학생이름만으로 바로 알 수 없다.
이와 같이 어떤 속성 A의 값을 알면 다른 속성 B의 값이 유일하게 정해지는 의존 관계를 '속성 B는 속성 A에 족송한다'
혹은 '속성 A는 속성 B를 결정한다' 라고 한다. 이 관계를 A->B로 표기하면 , A는 B의 결정자라고 한다.
학생수강성적 릴레이션에서 종속관계에 있는 예는 다음과 같다.
학생번호 -> 학생이름
학생번호 -> 주소
강좌이름-> 강의실
학과-> 학과사무실
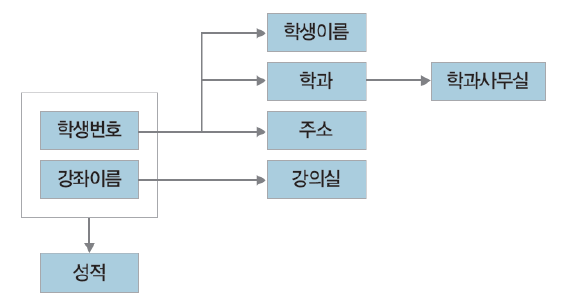
▶함수 종속성 다이어그램
함수 종속성을 나타내는 표기법으로 함수 종속성 다이어그램이 있다. 함수 종속서 다이어그램은 릴레이션의 속성을 직사각형, 속성 간의 함수 종속성을 화살표로 나타낸다. 복합 속성의 경우 직사각형으로 묶어서 그린다.
▶함수종속성 규칙
| 적용 규칙 | 사례 | 설명 |
| 부분집합 규칙 if Y⊆X, then X → Y |
(학과, 주소) → 학과 | 학과는 (학과, 주소)의 부분집합 속성이므로, '(학과, 주소) → 학과' 성립 |
| 증가 규칙 if X→Y, then XZ → YZ |
(학생번호, 강좌이름) → (학생이름, 강좌이름) |
'학생번호 → 학생이름'이므로 강좌이름을 추가하여, '(학생번호, 강좌이름) → (학생이름, 강좌이름)' 성립 |
| 이행 규칙 if X→Y and Y→Z, then X →Z |
학생번호 → 학과사무실 | '학생번호 → 학과', '학과 → 학과사무실' 이므로 이행 규칙을 적용하여, '학생번호 → 학과사무실' 성립 |
| 결합 규칙 if X→Y and X→Z, then X →YZ |
학생번호 →(학생이름, 주소) | '학생번호 → 학생이름', '학생번호 → 주소' 이므로 결합 규칙을 적용하여, '학생번호 → (학생이름, 주소)' 성립 |
| 분해 규칙 if X →YZ, then X→Y and X→Z |
학생번호 → 학생이름. 학생번호 → 주소 |
'학생번호 → (학생이름, 주소)' 이므로 분해하여, '학생번호 → 학생이름', '학생번호 → 주소' 성립 |
| 유사이행 규칙 if X→Y and WY→Z, then WX→Z |
(강좌이름, 학생이름) → 성적 | '학생이름 → 학생번호'(같은 이름이 없다고 가정) '(강좌이름, 학생번호) → 성적' 이므로 유사이행 규칙을 적용하여, '(강좌이름, 학생이름) → 성적' 성립 |
▶함수 종속성과 기본
테이블 R에서 K가 기본키이면, K -> R이 성립한다. 즉 기본키는 릴레이션의 모든 속성에 대한 결정자이다.
▶이상현상과 결정자
이사현상은 한 개의 릴레이션에 두 개 이상의 정보가 포함되어 있을 때 나타난다.
학생수강성적 릴레이션의 경우 학생 정보(학생번호, 학생이름, 주소, 학과)와 강좌 정보(강좌이름, 강의실)가 한 릴레이션에 포함되어 있기 때문에 이상현상이 나타난다.
이상현상은 기본키가 아니면서 결정자인 속성(비후보키 결정자 속성)이 있을 때 발생한다.
위의 함수 종속성 다이어그램을 보면 결정자는 '(학생번호, 강좌이름)', '학생번호' , '강좌이름', '학과' 다.
'(학생번호, 강좌이름)'는 기본키면서 결정자다.
'학생번호' , '강좌이름', '학과' 는 기본키가 아니면서 결정자다. 이로 인해 이상현상이 발생한다.
여기까지가 정규화를 이해하기 위한 개념들이다.
정규화에 대한 개념은 링크로 걸어 둔 블로그에 잘 나와있다.
[Database] 정규화(Normalization) 쉽게 이해하기
지난 포스팅에서 데이터베이스 정규화와 관련된 내용을 정리했었다. 하지만 해당 내용이 쉽게 이해되지 않는 것 같아서 정규화 관련 글을 풀어서 다시 한번 정리해보고자 한다. 1. 정규화(Normaliz
mangkyu.tistory.com
▶무손실분해
이렇게 이상현상을 제거하기 위해 정규화 할 때 지켜야 할 규칙이 있다.
분해된 릴레이션 간의 관계를 유지하기 위해 분해된 릴레이션에 공통 속성을 한 개 이상 두어야 한다는 것이다.
공통 속성은 분해된 릴레이션을 다시 원래의 릴레이션으로 합성(조인)할 때 사용한다.
무손실 분해의 조건은 분해할 때 공통된 속성(R1 ∩ R2)이 릴레이션 R1의 키이거나 (R1 ∩ R2 -> R1)
혹은 릴레이션 R2의 키 (R1 ∩ R2 -> R2)여야 한다.
이 규칙을 위배하면 두 개의 릴레이션을 조인할 때 원래 릴레이션에 없던 튜플이 생겨 잘못된 정보를 제공한다.
참고
'부트캠프 기록 > Serction2' 카테고리의 다른 글
| MySQL 설치 오류: installer 중단 (0) | 2022.10.08 |
|---|---|
| MySQL 실행 오류: Could not acquire management access for administration, MySQL 서비스가 로컬 컴퓨터에서 시작했다가 중지되었습니다. (0) | 2022.10.08 |
| [데이터베이스] SQL DB Schema (0) | 2022.10.07 |
| [데이터베이스] SQL (0) | 2022.10.06 |
| [네트워크]HTTP통신 (0) | 2022.10.05 |